[논문리뷰] Neural Collaborative Filtering (1)
본 글은 Neural Collaborative Filtering (NCF) 논문을 리뷰해볼 것이다.
해당 논문은 기존 CF의 가장 강력한 알고리즘으로 자리잡고 있던 MF(Matrix Factorization) 방법에 대해 한계점을 짚고,
이를 Neural Network기반으로 풀어가면서 어떤 개선을 할 수 있는지를 담고있다.
논문을 본격적으로 리뷰하기 전에 상품 추천 시스템에 대해 좀 더 알아보면,
상품 추천 시스템으로는 세 가지 타입이 있다.
1. User-Product : 개인의 선호에 따라 상품 추천
2. User-user : 유사한 상품 선호를 가졌을 것이라 추정되는 사람간의 상품 추천
3. Product-product : 보충적인 성격을 지닌 상품끼리의 추천
1번의 경우 완전히 개인화된 상품 추천 시스템이라 볼 수 있고,
2번의 경우 일반적으로 개인화된 행동 이력이 아직 수집되지 않은 신규 유저들을 대상으로 하는 추천 모델이 될 수 있다.
마지막의 경우 유사 상품 추천시에 이용해볼 수 있는 모델 타입이다.
이처럼 각각의 성격별로 서비스 내에 녹일 수 있는 범위가 다르다.
이러한 상품 추천 시스템에 사용되는 머신러닝 알고리즘은 아래와 같이 리스팅해볼 수 있다.
1. Collaborative Filtering (CF)
2. Content-based Filtering (CBF)
CF의 경우 가장 유명한 알고리즘으로서, 협업 필터링이라고 부르는데,
A라는 유저가 속성 1~K까지의 선호를 지닐 때, 유저 B에 대해서 A의 선호 속성을 기반으로 추천을 제공할 수 있는 것이다.
KNN 알고리즘이나 LFM(Latent Factor Analysis) 등을 사용하곤 한다.
유사한 상품을 찾아내는 Item-based 알고리즘과 유사한 그룹(neighbor)을 탐색하는 User-based 알고리즘으로 나뉘어진다.


recommenderlab 논문 발췌
Content-based Filtering의 경우 상품을 구매한 내역, 클릭한 내역 등의 컨텐츠를 바탕으로 Profile을 구성하고, 추천하게 된다.
CF, CBF 두 가지 모델을 혼합하여 만든 Hybrid recommendadtion system 도 존재한다.
이번 논문은 CF기반인데, 기존에 사용하던 MF가 아니라, 딥러닝을 기반으로 하는 모델을 설명하고 있다.
기존 MF 로직은 user과 item간의 feature들을 내적(inner product)을 통해 계산하고 있다.
이러한 방식은 Linear한 데이터를 가정하고 있고, 유저와 아이템간의 복잡한 관계를 설명하기에 충분하지 않다고 말한다.
반면 Neural Network는 non-linear한 관계도 표현이 가능하기에, MF의 한계점을 뛰어넘을 수 있다고 한다.

논문 그림 발췌 : (a)에서는 u4가 u1 > u3 > u2 순으로 가까운 것으로 보이나, (b)와 같이 표현하게 될 경우, p4를 p1에 가깝게 배치하면서 p4와 p2간의 간격차가 좁혀지면서 ranking에 loss가 발생한다. 즉 p1과 가장 가까우면서 p2와 가장 먼 p4는 없는 것이다. 이는 linear space의 한계이다.
첨부된 그림과 함께, 좀 더 수학적으로 살펴보면 MF의 연산로직은 아래와 같다.
$\combi{y}_{u,i}=f(u,i\ |\ \combi{p}_u\ ,\ q_i)=\combi{p}_u^T\ q_i=\sum _{k=1}^K\combi{p}_{uk}\ q_{ik}$yu,i=f(u,i | pu , qi)=pTu qi=K∑k=1puk qik
위와 같이 유저 u와 아이템 i에 대한 latent factor Pu, Qi를 서로 내적한 것을 interaction 값으로 사용한다.
이와 같은 방법은 latent space의 dimension K내에 있는 모든 latent factor가 서로 독립적이라는 것을 가정하고 있고,
이들을 결합할 시에도 동일한 weight값으로 linear하게 연산하고 있다.
즉 user-item간의 복잡한 관계를 MF는 저차원 latent space에서 표현하려다 보니 한계점에 부딪히는 것이다.
더 나아가 논문은 Implicit Feedback에 대해 이야기하고 있다.
예를 들어 평점과 리뷰와 같은 명확한 선호는(Explicit Feedback) 개인의 성향을 파악하기 쉬우나,
클릭을 했다던지 조회를 했다는 불명확한 데이터를 기반으로 개인의 선호를 파악하기 위해서는 DNN 로직이 더 좋다는 것이다.
조금 제너럴하게 말하고 있어, 좀 더 살펴보도록 하자.
m명의 유저와 n개의 Item이 있다고 하자. 그럼 user-item 행렬은 아래와 같이 구성이 될 수 있다.
$\combi{Y}_{m,n}\ =\left(\begin{matrix}\combi{y}_{1,1}&\cdot \cdot \cdot &\combi{y}_{1n}\\\cdot \cdot \cdot &\cdot \cdot \cdot &\cdot \cdot \cdot \\\combi{y}_{m,1}&\cdot \cdot \cdot &\combi{y}_{m,n}\end{matrix}\right)$Ym,n =(
| y1,1 | ··· | y1n |
| ··· | ··· | ··· |
| ym,1 | ··· | ym,n |
)
$where,\ \combi{y}_{u,i}=\left\{\begin{matrix}1,\ if\ interaction\ \left(user\ u,\ item\ i\right)\ is\ observed\\0,\ otherwise\end{matrix}\right\}$where, yu,i={
| 1, if interaction (user u, item i) is observed |
| 0, otherwise |
}
$$
행렬 각각의 원소 값은 1일 때는 user u와 i간의 상호작용이 있었다는 것인데, 문제는 0일 때 u가 i를 좋아하지 않는다고 판단하기 어렵다는 것이다.
단순히 유저가 아이템 i에 대해 인지하고 있지 않은 상태일 수도 있기 때문이다. 이것이 바로 implicit feedback이다.
이러한 implicit feedback이 있을때, 모델은 결국 유저 u가 item i를 선호할 확률 y 값을 구하는 문제를 풀게 되는 것이다.
Objective Function이 위와 같이 정의되었을 때, loss function은 아래와 같이 두 가지로 사용해볼 수 있다.
$L1=\min _{ }^{ }\ \frac{1}{2}\left(\hat{\combi{y}_{u,i}}\ −\ \combi{y}_{u,i}\right)^2$L1=min 12(^yu,i − yu,i)2
$L2=\max _{ }^{ }\ (0,\ \ f(\combi{y}_{unobserved})−f(\combi{y}_{observed})+\alpha )\ \ $L2=max (0, f(yunobserved)−f(yobserved)+α)
L1은 point-wise loss function으로, 실제 값과 예측 값간의 차이를 제곱한 것으로, 주로 회귀 분석에 사용된다.
L2는 pair-wise loss function으로, 관측된 값과 관측되지 않은 값 간의 마진 차이를 최대로 하도록 하는 것이다.
본 논문은 DNN 알고리즘을 취하고 있어 두 loss function을 자연스레 취하게 된다고 한다.
NCF 모델의 구성은 아래와 같다.
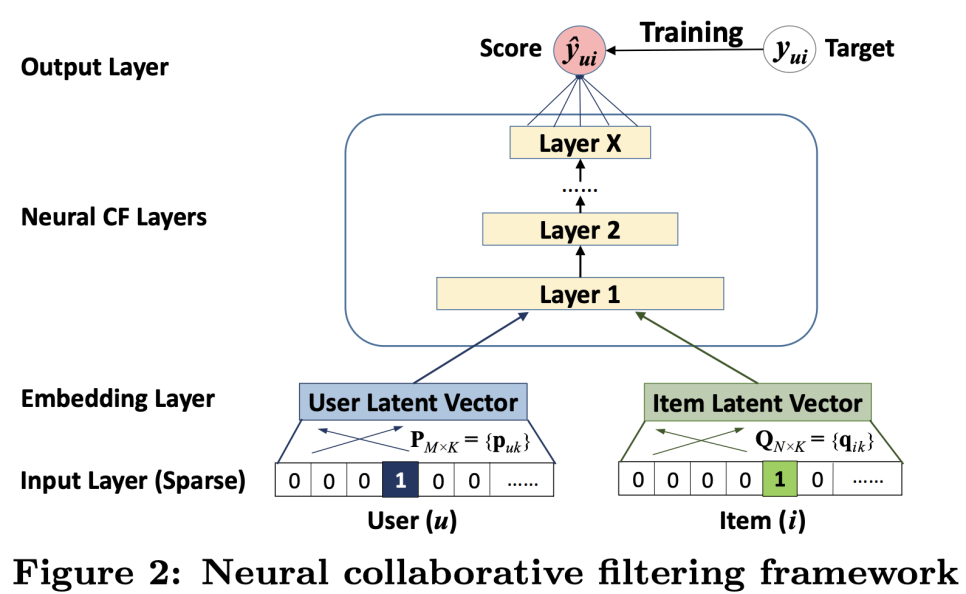
논문 발췌
우선 User과 Item에 대한 latent vector를 one-hot encoding을 통해 생성한다.
그 후 Embedding Layer을 통해 Input에서 들어온 sparse한 벡터를 dense한 vector로 뱉어내게 된다.
Embedding Layer는 별도의 Fully-connected neural network로 구성되어 있고,
M차원의 User Latent Vector를 M보다 저차원인 벡터로 변환하여 반환한다.
그 후 Neural CF Layer라고 명명되어 있는 X층의 Layer를 통해 예측된 스코어 값과 타겟 스코어 간의 마진을 최소화하도록 학습하고,
최종적으로 예측된 Y값을 내뱉게 되는 구조로 되어있다.
이처럼 NCF모델은 유저 u와 아이템 i에 대한 y 라벨값을 아이템 i가 유저 u와 관련이 있다는 의미로서 사용하고,
예측 값은 아이템 i가 얼마나 유저 u와 연관이 있을건지에 대한 의미를 내포하고 있다.
이 값은 [0, 1]의 범위를 가지기 때문에 이진 분류 문제로 볼 수 있다.
본 모델은 GMF(Generalized Matrix Factorization)와 MLP(Multi Layer Perceptron) 두 기술을 혼합하여 사용한다.
* GMF
GMF는 MF와 유사한데, generalized된 NCF의 MF 알고리즘을 의미한다.
논문은 NCF모델에서 embedding layer가 MF와 유사한 성격을 띠고 있다고 말한다.
one-hot 인코딩된 유저/아이템 벡터가 유저/아이템에 대한 latent vector라고 볼 수 있기 때문이다.
$\hat{^yu,i}=\combi{a}_{out}(\combi{h}^T(p_u\Theta \ \combi{q}_i))$^yu,i=aout(hT(puΘ qi))
여기서 a는 activation 함수이고, h는 output layer의 edge weight이다. (p는 유저 벡터, q는 아이템 벡터)
이 때 a가 identity 함수이고, h를 1인 uniform vector라고 하면 MF와 동일하다.
a가 non-linearity를 살려주고, h가 latent dimension을 강조해주는 셈이다.
a를 sigmoid function으로 정의하고, h를 log loss로 사용하는 모델을 GMF로 정의하고 있다.
* MLP
앞서 기존 방식인 MF가 복잡한 user-item간 상호작용을 설명하기 충분하지 않다고 이야기했었는데,
이를 해결할 수 있는 방법으로 MLP를 제시하고 있다.
아이템과 유저간의 상호작용을 학습할 수 있도록 MLP가 모델에게 유연성과 non-linearity를 높은 수준으로 부여해줄 수 있다는 것이다.
GMF는 단순히 원소끼리 곱하도록 고정되어 있기 때문에 제한적이다.
* MLP의 활성화 함수는 ReLU를 사용하는 것으로 하였다.
즉 latent feature를 모델하는 선형 커널인 GMF와 데이터와 목적함수간 상호작용을 학습할 비선형 커널인 MLP를 합치는 것이다.
이 두 모델을 embedding layer를 공유함으로써 합칠 수 있다.

논문 발췌
위와 같이 NMF 구조를 이용한 NCF는 MF의 linearity와 MLP의 non-linearity를 함께 활용하여
유저와 아이템간의 복잡한 상호작용을 implicit 데이터를 기반으로도 추천할 수 있도록 설계되었다.
다음 글에서는 이 모델을 어떻게 구현할 수 있는지에 대해 살펴볼 것이다.
참고자료
https://www.netguru.com/blog/product-recommendation-machine-learning
How to Build a Product Recommendation System using Machine Learning
A product recommendation system is a software tool designed to generate and provide suggestions for items or content a specific user would like to purchase or engage with. With machine learning techniques, the system creates an advanced net of connections between those products and those people.
www.netguru.com
https://leehyejin91.github.io/post-ncf/
[논문 리뷰] Neural Collaborative Filtering
Recommender System
leehyejin91.github.io