MAB - 넷플릭스 artwork personalization 사례
넷플릭스에서는 영상 이미지, 즉 artwork를 어떤 것을 선택할지에 대해 추천 로직을 적용하고 있다.
이미지는 대표성과 정보성, 매력, 차별성을 지니고 있어야하는데, 이 모두 개인적인 성향에 영향을 받을 수 밖에 없다.
사람들은 대개 장르 혹은 캐스팅에 대한 선호를 지니는데, 이 선호가 이미지로 반영될 수 있다.
행과 열로 구성된 바둑판 화면을 inventory라고 치면, 각 구좌에 배치할 오더링과, 구좌에 넣을 광고 이미지는 어떤 것을 선택해야할까?
이 모든 것은 추천 알고리즘으로 돌아간다.
전통적인 추천 방식은 단연 Collaborative Filtering 이다. 하지만 이로 부족하다.
CF는 현재 운영중인 상품 pool 내에서만 유사한 상품 추천이 가능하고, 새로이 탐색할 수 있는 방법이 없다.
새로운 상품이 유입되면 cold-start 문제로 적절히 추천해줄 수 없다.
또한 사람들의 선호는 실시간으로 바뀌고, 반응하였을 경우 rating을 매기지,
모델 입장에서는 rating에 따라 특정 유저가 반드시 그 영화를 선호/불호했다고 단언할 수 없다.(implicit feedback)
A, B, C 가 노출되었을 때 A를 선택했다고 하더라도 반드시 A를 선호하고 있다고 단정할 수 없고, 그 외 영화들을 비선호한다고 볼수도 없다.
이러한 맥락에서 추천 문제를 MAB에 접목하였다.
학습자는 지속적으로 action하고, 그에 대한 reward를 받는다. 이 때 학습자는 누적 보상값을 최대화하는 방향으로 행동해나간다.
넷플릭스도 동일하게 작동하는데, 사람들은 홈페이지에서 마음에 드는 artwork를 선택하고, 알고리즘은 매칭률을 높이는 방향으로 업데이트한다.
Bandit은 각 action에 대한 optimial 보상과 선택된 보상의 간차를 줄이는 것을 목표로한다.
Metric은 반응 수 / 노출수로 잡게 되는데, 예를 들어 영화 A에 대해 4명의 유저에게 보여주고 2명이 반응하였다면 2/4 를 관측치로 사용한다.
이렇게 전체 영화에 대해 관측치를 계산하고 나면, 두 전략 사이에 고민이 발생한다.
1) 현재 경험상 가장 best 선택지를 고른다
2) 아직 경험해보지 못한 선택지를 골라 경험을 쌓는다
1)을 Maximization/Exploitation전략, 2)를 Exploration전략으로 부른다.
2)는 장기적으로 가장 좋은 선택을 할 수 있게끔 정보를 쌓는다는 장점이 있다.
데이터를 모으는 것이 결국엔 초기에 탐험에 소요된 시간이나 비용을 보상하게 된다고 생각한다.
어느 정도로 탐색하고, 어느정도로 수확해야할까? 내가 탐색을 통해 찾은 전략이 optimal 하다고 볼 수 있을까?
이러한 상황에서 취할 수 있는 전략은 아래와 같다.
A. 단순히 Exploration을 지속한다 (Naive Exploration)
B. 불확실하지만, Optimize해나간다 (Optimism)
C. 확률분포를 통한 유추 (Probabilstic)
A 를 취하는 알고리즘으로 e(입실론)-greedy가 있다. 바로 입실론 확률만큼 exploration하는 것이다.
초기에는 탐색을 진행하고, 일정 시간 이후 분기를 정하여 입실론만큼 탐색하고 그 외의 suboptimal 액션에 대해 수확한다.
알고리즘이 간단하다는 장점이 있지만, 오차가 무한할 수 있다는 단점이 있다.
가장 좋은 보상이라고 생각하는 것이 사실상 optimal하지 않을 수 있기 때문이다.
B 를 취하는 알고리즘으로는 UCB(Upper Confidence Bound)가 있다.
지금껏 관측된 결과에 따라 예측된 보상의 신뢰도를 계산한 후, 신뢰도의 Upper Bound가 가장 높은 action을 취한다.
해당 액션에 대한 결과를 다시 업데이트하여 신뢰도를 재계산한다.
이 알고리즘은 지금껏 탐색한 action들에 대한 보상 뿐만 아니라, 해당 보상이 얼마나 불확실성을 가지고 있는지까지 추정하게 된다.
즉 action별 최고 성과에 대한 기록과, 각 보상을 얻기까지 얼마나 많은 탐색을 거쳤는지 (=즉 얼마나 불확실성을 지니는지)도 따지게 된다.
장점은 이론적으론 오차를 optimize해나간다는 것이지만, 단점은 관측된 값을 재빠르게 업데이트해줘야한다는 것이다.
예를 들어 아래 그림에서 왼쪽의 경우 2번 action이 가장 높은 UCB를 갖는다. 그래서 2번을 선택하여 얻은 결과로 신뢰도를 update한다.
하지만 대개의 경우 불확실성이 가장 큰 action이 UCB를 지닐 것이다. 따라서 오른쪽 그림과 같이 1번이 action으로 선택되고, 이 1번은 일정정도의 exploration을 통해 UCB가 현재에 비해 줄어들 것이다. 이 과정이 바로 불확실한 보상에 대해 더 많은 탐색을 진행하게 되는 과정이다.
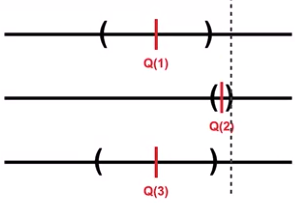

출처 : https://jyoondev.tistory.com/137
만약 각 artwork에 대한 베타 분포를 이용하여 UCB 알고리즘을 적용해본다면,
아래와 같이 a, b, c 세 영화에 대해 각각 관측된 반응값에 따라 베타 분포를 만들어준다.
베르누이 분포의 p값을 클릭/반응으로 잡고 본다면, 사전 확률 분포는 p의 분포와 동일하다. (0 <= p <= 1 )

데이터를 어느정도 수집하였으니 사후 확률 분포를 그려볼 수 있는데, a,b,c에 대해 클릭 이력을 input하여 베타 확률 분포를 그린다.
베타 확률 분포는 일반적으로 비율을 설명할 때 사용되고, 파라미터로는 알파와 베타를 받는다.
B(x; a, b) 구조인데, x를 반응률로 잡게 되면, 특정 a, b값에 따라 반응률이 x1 ~ x2구간 사이에 위치할 확률을 구할 수 있다.
위 그림에서는 a는 영화별 클릭수, b는 총 클릭 수로 잡고, x는 반응률/클릭률로 잡은 것이다.
그래프를 그렸으니 신뢰도를 정한 뒤(ex. 95%) 각 신뢰구간을 구하여 가장 높은 UCB를 지닌 분포도의 영화를 선택하는 것이다.
C를 취하는 알고리즘은, 요즈음 가장 다수의 곳에서 사용되는 Thompson Sampling이다.
각 action이 최선일 것이라는 확률에 따라 action을 취하는 것이다.
즉 각 action에 대해 확률분포를 그린 뒤, 샘플을 각 분포에 넣어 예측된 보상값을 비교한다.
이 보상값을 선택하여 행동을 취한 뒤, 얻은 결과로 다시 분포를 업데이트해나가는 것이다.
아래 예시를 보면 a, b, c 세 action에 대해 각각 관측된 결과에 따른 확률분포를 plotting하고, sampling을 통해 얻은 결과를 바탕으로 각 분포를 수정해나가는 것을 확인할 수 있다.
결과적으로 1000번의 시행 이후 각 action에 대한 실제 보상과 유사한 확률분포를 그릴 수 있다는 것이다.

출처 : https://towardsdatascience.com/thompson-sampling-fc28817eacb8
UCB와는 달리 확률분포를 바탕으로 랜덤 sample을 추출하게 되어 좀 더 확률적으로 최대의 보상을 찾아나갈 수 있다는 접근이다.
예를 들어 UCB는 관측된 결과 중에서 가장 높은 영화를 먼저 선택하게 되어, 그 그래프를 업데이트해나가는 방향이지만,
Thompson sampling은 그와는 다르게 샘플링에 따라 랜덤하게 추출됨으로 관측된 결과 중 가장 최악의 선택을 먼저 추천해줄 수도 있다.
Contextual Bandit
Netflix는 artwork 추천에 Bandit을 적용해보니 아래와 같은 장애물을 마주한다.
1) 선택에 따른 보상값이 실시간으로 변한다
2) 보상이 어떻게 생성되었는지에 대한 설명을 할 수 없다
3) action이 무한가지이고, 각 action도 시간에 따라 변한다
즉 Bandit은 여러가지 action을 취할 수 있게 해줬지만, 개인화된 추천을 하진 않았던 것이다.
개인화된 추천이란 영화의 장르에 대한 선호나, 영화에 등정하는 배우에 대한 선호 등 개인의 context정보가 없는 것이다.
이에 따라 Contextual Bandit을 고민해보기 시작했다.
앞서 살펴본 Bandit모델에 context라는 새로운 feature가 생긴 것이다. Context는 사용자의 디바이스, 사용자 성별 등이 해당할 수 있다.
앞서 살펴본 세 가지 알고리즘을 다시 contextual bandit에 적용해보자.
각 영화별로 이미 관측된 행동들과 context를 feature로 사용하여 보상의 확률분포를 예측하는 모델들을 세우게 되고,
A - epsilon greedy : 입실론 확률만큼 이미지를 랜덤으로 뿌리고(exploration), 그 외의 확률로 개인화된 이미지를 보여준다. (exploitation)
B - UCB : LinUCB알고리즘, 즉 각 이미지별로 보상을 예측하는 선형(linear) 모델을 세워 특정 percentile 내 상위값을 지닌 모델을 선택한다.
C - Thompson Sampling : 베이지안 회귀분석과 같은 모델을 세워 확률분포를 예측한 뒤, 각 분포에서 샘플링하여 최선의 선택을 취한다.
Bandit 모델로 서비스를 서빙하게 되면 고려해야할 사항들이 있다.
우선 가장 처음엔 모델을 서빙하지 않고, 데이터를 수집해야한다.
유저가 제공하는 보상을 저장하고, 어느정도 데이터가 쌓이게 되면 모델을 학습하여 추론된 결과로 추천해야한다.
또한 실시간으로 추천해줄 것인지, 아니면 온라인으로 저장된 데이터로 추천해줄 것인지를 선택해야한다.
물론 실시간으로 추천해주면 신선함이 반영되지만 response가 제때 도착해야하고, scalability가 보장되어야한다.
반면 대량의 데이터를 캐싱해두고 저장된 데이터로 추천하게 되면, 큰 데이터를 handling할 수 있지만 신선도는 떨어질 수 있다.
아키텍쳐 구성도 중요할 것이고, 선호 변화에 따른 로직 구성도 잘 짜여져있어야 한다.
예를 들어 개인화된 추천에 대한 반응이 좋지 않았다면, 개인화를 제외한 추천(degraded)을 하고, 그래도 반응이 좋지 않으면 default이미지를 제공하는 등의 로직이 마련되어있어야한다. 최상의 선택을 제공하기 위해서다.
본 글에서는 추천 시스템 알고리즘 중 Bandit계열 알고리즘들을 간단하게 살펴보고, Netflix에서는 어떻게 활용하고 있는지 확인할 수 있었다.
다음 글에서부터는 각 알고리즘에 대한 상세 로직과 contextual bandit에 대해 좀 더 살펴볼 것이다.
참고자료
https://qconsf.com/system/files/presentation-slides/2018-11_-_qcon_artwork_personalization_talk.pdf
https://netflixtechblog.com/artwork-personalization-c589f074ad76
Artwork Personalization at Netflix
Artwork is the first instance of personalizing not just what we recommend but also how we recommend.
netflixtechblog.com
베타 분포
http://norman3.github.io/prml/docs/chapter02/1.html
1. Binary Variables
1. Binary Variables 우선 가장 간단한 형태의 식으로 부터 논의를 시작한다. 랜덤 변수 x 가 x ∈ { 0 , 1 } 인 상황(즉, 취할 수 있는 값이 단 2개)에서의 확률 분포를 살펴본다. 가장 간단한 경우가 바로 동전 던지기 예제인데, 동전을 던저 앞면이 나오면 x = 1 , 뒷면이 나오면 x = 0 이다. 이 때 이 동전의 앞,뒷면이 나올 확률이 서로 동일하지 않다고 하면 앞면이 나올 확률은 다음과 같이 정의할 수 있다. p ( x = 1 | μ ) = μ ( 2.1 ) 여기서 0 ≤ μ ≤ 1 이다. ( 이 ...
norman3.github.io
https://www.real-statistics.com/binomial-and-related-distributions/beta-distribution/
Beta Distribution | Real Statistics Using Excel
Beta Distribution Definition 1 : For the binomial distribution the number of successes x is a random variable and the number of trials n and the probability of success p on any single trial are parameters (i.e. constants). Instead, we would now like to view the probability of success on any single t...
www.real-statistics.com