추천시스템 - (2) One-class Collaborative Filtering
본 글에서는 추천 시스템 문제 중 하나인 One-class 협업필터링에 대해 정의를 짚고, 그를 해결하기 위한 알고리즘들을 간단하게 소개해볼 것이다.
One-class Collaborative Filtering이란
One-class collaborative filtering의 문제정의에 대해 살펴보자.
Input은 사용자의 implicit한 피드백을 받고, output으로는 사용자의 top N 상품을 추천하는 것이다.
여기서 implicit한 피드백이라는 것은, 명확한 피드백이 아니라는 것인데, 즉 rating과 같이 직접적으로 유저가 선호를 매긴 것이 아니라는 것이다.
rating은 통상 1부터 5점까지 scaled된 점수를 매기게 되지만, implicit 피드백은 구매 이력이라던지, 브라우징 이력, 클릭 등 정보로 구성된다.

이에 따라 One-class 협업필터링은 rating setting보다 더 sparse한 데이터셋이다.
또한 rating setting보다 유저의 선호를 추정할 수 있는 정보가 적다.
One-class Collaborative Filtering 문제를 접근하는 방법은 크게 두 가지가 있다.
1. point-wise : 사용자의 아이템별 실제 스코어와 예측 스코어간 error를 최소화하는 목적함수를 사용
2. pair-wise : 사용자의 rated item과 unrated item간의 예측 스코어 차이를 극대화하는 목적함수를 사용
Matrix Factorization 계열 알고리즘
우선 point-wise 계열 알고리즘에 대해 살펴보자.
WRMF : Wiehgted Regularized Matrix Factorization 알고리즘이 point-wise 접근 방식의 알고리즘 중 가장 유명하다.

Unary rating matrix에서 Unary란 binary와 다르게 알고 있는 정보가 한 가지 밖에 없기 때문이다.
즉 사용자가 rating하지 못한 것은 알지 못한 정보로 보기 때문에 0으로 매기지 않는다.
WRMF는 Unrated item을 negative preference로 가정하고 단순하게 값을 0으로 매기고, rating matrix외에 weight matrix를 생성한다.
Weight matrix란 rating matrix 값에 대한 신뢰도(confidendce) 값으로 만들어진다.
이 때 positive rating에 대해서는 max값인 1로 매겨지고, 나머지 0으로 매겨진 값에 대해서는 confidence값으로 채워진다.
weight matrix는 이름에서도 유추 가능하듯이 추천 결과에 있어서 weight가 높은 항목에 대한 예측에 좀 더 중요성을 가중하는 방식이다.
pair-wise로 유명한 알고리즘은 BPR이라고 있다. BPR은 Bayesian Personalized Ranking from Implicit Feedback의 줄임말이다.

목적함수 식에서 +는 산 아이템, -는 안 산 아이템을 의미하는 notation이다.
즉 Rated Item과 Unrated item 두 스코어 차이에 대해 극대화하는 방식이 BPR이다.
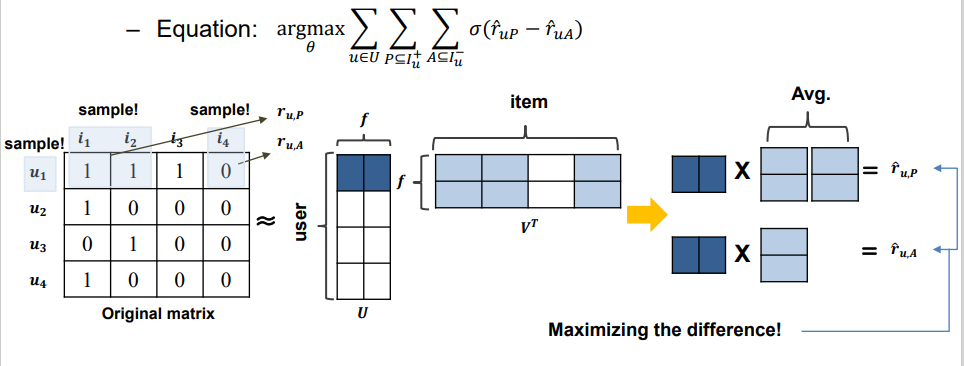
CoFiSet(Collaborative Filtering via Learning Pairwise preferences over a pair of item-sets)이라는 알고리즘도 있다.
이는 아이템과 아이템 간 차이를 보는 것 보다, unrated item set과 rated item set간의 차이를 보는 것이 더 안전하다고 생각한다.
사용자가 산 아이템 중 그룹을 랜덤하게 묶고, unrated 아이템 중에서도 랜덤하게 그룹을 묶어 그 간 선호 차이를 극대화하는 방식이다.
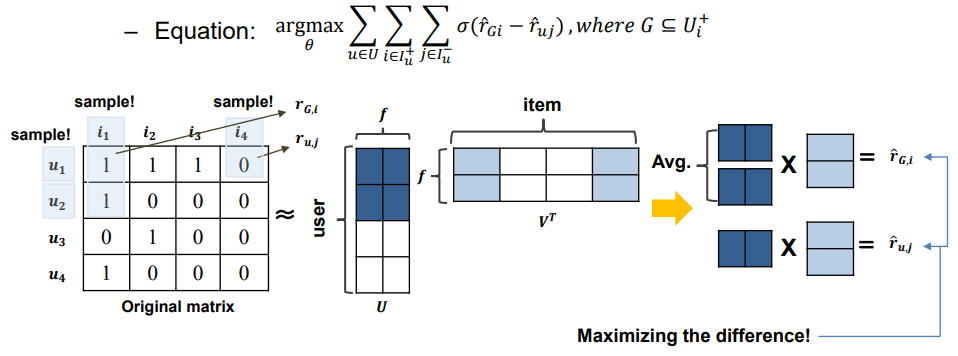
다른 pair-wise 계열 알고리즘으로는 GBPR이 있다. (Group based Bayesian Personalized Ranking)
유저 그룹의 선호를 도입한 알고리즘인데, A라는 사용자의 rated 아이템에 대한 선호에 대해 A 친구들도 마찬가지로 선호했을 경우 다른 unrated item보다 선호 차이가 클 것이라는 가정으로 접근한다.
아래 도식을 보면 알겠지만, 사용자 그룹의 rated item에 대한 선호가 unrated item에 대한 선호간의 차이를 극대화하는 것이다.
Deep-learning 계열 알고리즘
컴퓨터 비전이 2015년도 전후로 열풍을 일으키면서, 곳곳에서 NN기반 모델을 사용하기 시작했다.
추천 시스템에서도 DL기반 알고리즘들이 하나둘 씩 생기기 시작했는데, 그 중 시초는 AutoRec 이다.
Matrix기반으로 아이템 추천을 진행하게 되면, 결국 빈 공간의 데이터를 어떻게 활용할 것인가에 대한 문제가 계속 제기된다.
AutoRec은 본래의 matrix를 재구성한(reconstructed) matrix로 만드는 auto encoder를 발굴하는 문제인데, 재구성하는 이유는 unrated items에 대한 rating을 추정하여 데이터를 좀 더 풍부하게 사용하기 위함이 있다.
AutoRec은 Item-based AE와 User-based AE, 두 가지로 나뉘게 된다.
AE는 NN구조로 되어있고, 논문에서는 hidden layer가 깊을 수록 정확도가 높아진다고 말한다.
NeuCF 모델도 참고해볼만하다. 기존의 MF계열 모델들은 내적(inner product)로 연산하기 때문에 아이템과 유저간의 복잡한(not linear) 관계를 잡아낼 수 없다는 생각에서 시작되었다.
세 가지 층이 있는데, GMF, MLP, NeuMF 세 가지로 되어있다.
- GMF : Generalized Matrix Factorization
- MLP : Multi-Layer Perceptron
- NeuMF : Fusion of GMP & MLP
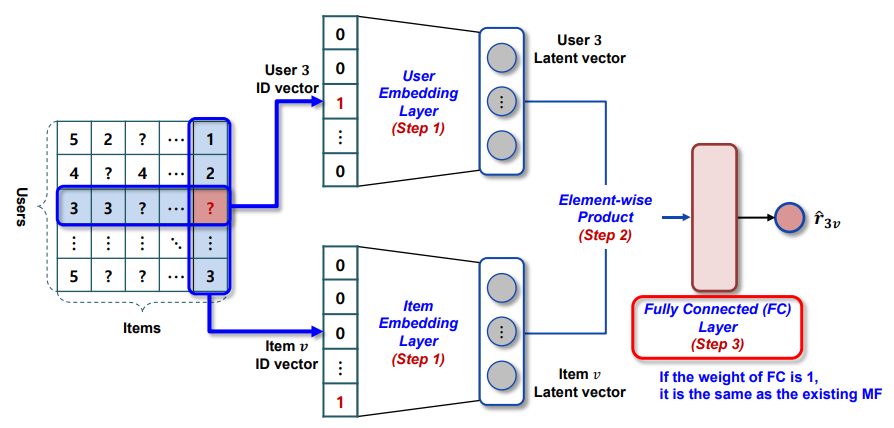
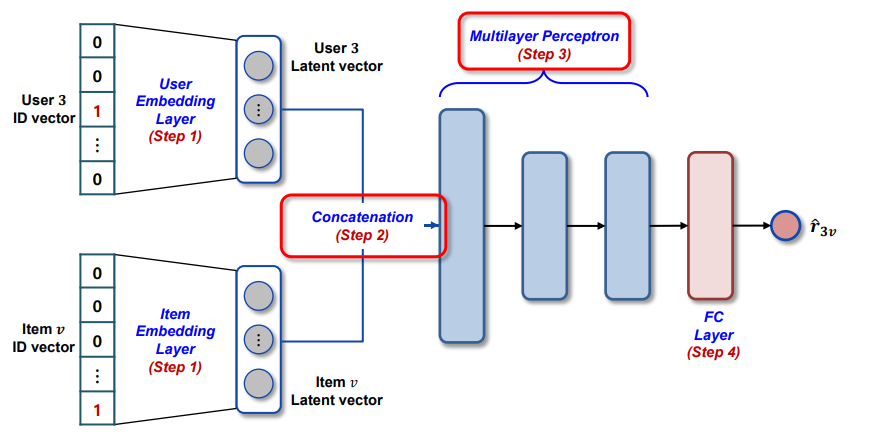
GMF와 MLP 를 concatenate하여 최종적으로 점수를 예측하게 된다.
이전에 블로그 글로 NeuMF 논문을 리뷰하여 쓴 글이 있어 아래 링크를 걸어두었다 :
https://blog.naver.com/ilovelatale/222338052899
GAN 계열 협업필터링 알고리즘들도 있다. 직관적으로 생각하면 어떻게 접목될 수 있을지 잘 감이 안올 수 있는데, 사용자가 선호할 것 같은 item 의 index를 생성하는 모델이다. 이 계열 모델에 대해서는 이정도로 소개만 하고 자세히 다루진 않겠다.
Graph 계열 알고리즘
그래프는 object들을 노드로 구성하고, 그 노드들 간의 관계를 edge로 표현한 데이터 구조이다. 추천 시스템에서도 graph를 사용한 알고리즘들이 있는데, 그 중 RWR (Random Walk with Restart)과 BP (Belief Propagation)를 살펴보자.
RWR (Random Walk with Restart)은 두 단계로 나뉘게 되는데,
- Random Walk : 시드 노드로부터 다른 노드 간의 연관도가 얼마나 있는지를 연산하는 단계. (1-알파) 확률로 edge를 통해 다른 노드를 랜덤하게 pick
- Restart : 알파 확률로 target 노드로 다시 돌아오는 단계
즉 어떤 시작 노드를 기점으로 출발하여 랜덤한 간선(edge)를 선택하여 이웃 노드로 움직이면서 각 노드를 방문하게 될 확률을 구하는 것이다.
어느 정도 RWR을 순환해보면 노드 방문 확률이 어느 정도의 값으로 수렴하게 되는데, 이 값이 높을 수록 노드를 방문할 확률이 높다, 즉 선호가 높다고 볼 수 있다는 주장이다.
주로 웹 검색결과 추천으로 사용되는 page rank 알고리즘으로 사용되는데, 연관 웹페이지와 그 연관도를 계산할 때 사용된다.
Belief Propagation (BP)은 근접 노드의 status에 따라 특정 노드의 state를 추론하는 방법이다.
이 때 Message passing이라는 기법이 사용되는데, "내가 X라는 상태(state)에 있다면, 내 주변 이웃의 state는 어떠할까?"라는 질문을 던진다. 이러한 정보가 노드들 간에 서로 오가면서, message value가 어느 수준의 값으로 수렴하게 된다면 알고리즘의 순환이 종료된다.
NGCF(Neural Graph Collaborative Filtering)은 유저-아이템 그래프의 high-order connectivity를 모델링하는 알고리즘이다.

그림과 같이 유저1과 i2, i3을 동일하게 interact한 유저 2, 3이 아이템으로 연결되어있다. 이 그래프에 따라 유저1은 아이템 4도 선호할 것이라고 예측해볼 수 있는 것이다. 이처럼 high-order connectivity를 연산하는 과정은 Graph Convolutional Network(GCN) 이라고 부르게 되는데, 우선 노드와 엣지로 구성된 그래프와 근접성(adjacency) matrix와 node-feature matirx, 세 가지를 셋팅한다. 이 때 각 그래프의 노드들로 구성된 embedding vector를 구하는 것이 최종 목표이다.
embedding vector 는 몇 번의 iteration을 거쳐 업데이트되는데, 그 과정은 아래 그림으로 설명된다.

Aggregate란 특정 노드 v의 인접 노드들의 정보를 모으는 것이고, combine은 그 정보를 합쳐 v만의 정보로 만드는 것이다. 이렇게 사용자와 아이템에 대한 embedding vector를 만들게 되면, 그를 서로 dot product하여 선호를 추정하게 된다.
최초의 유저와 아이템 embedding vector 과 각 iteration(layer)에서 반환된 embedding vector를 모두 최종적으로 concatenate한다. NGCF는 non-linear한 activation(LeakyReLU함수)를 사용한다는 점과 큰 사이즈의 user-item interaction 그래프에서는 성능을 충분히 낼 수 없다는 단점이 있다. 이러한 NGCF의 단점을 보완하여 새롭게 제안된 모델 lightGCN도 있다. 요즈음은 좀 더 성능이 좋고 속도가 빠른 lightGCN을 다수 사용한다.
Metric Learning 계열 알고리즘
MF계열 알고리즘과 MLP계열 알고리즘 모두 inner product 연산을 포함하고 있는데, 이는 metric learning 접근방식과는 조금 다르다.
내적은 "triangle inequality"를 만족하지 못하기 때문이다.
Metric Learning 접근방식은 아래와 같은 특성을 만족해야한다.
아래에서 d라는 notation은 distance를 의미하며, i, j 는 각각 특정 장소 혹은 노드 라고 생각하면 된다.
하나씩 읽어보면 조금 직관적인데, 3번에 대해서만 설명을 해보면,
i와 k 가 서로 멀지 않고, k와 j가 서로 멀지 않다면, i와 j간의 거리도 멀지 않다는 것이다.
이를 추천과 연관시켜 생각해보면, i와 k라는 사용자와 k와 j라는 사용자 간의 선호가 유사하다면, i와 j 사용자의 선호도 유사하다는 것이다.

즉 내적하는 방식으로는 유사 아이템에 대한 사용자의 선호를 잡아내기 충분하지 않다는 이야기이다.
Metric Learning은 사용자와 아이템을 저차원의 metric 공간으로 표현한다.
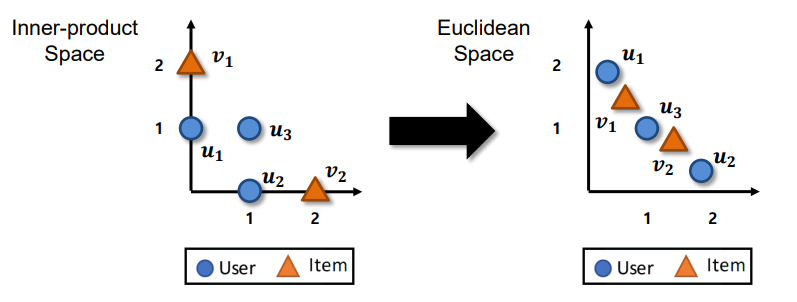
위의 Metric공간에 풀어낸 아이템과 유저 간의 euclidean 거리를 최적화하는 것이 Metric learning의 학습 방향이다.
이 계열 알고리즘 중 CML을 살펴보자.
CML은 유저에게 긍정적인 아이템은 유저 근처에 두고, 유저가 좋아하지 않는 아이템은 특정 margin 밖으로 보내도록 구성한다.
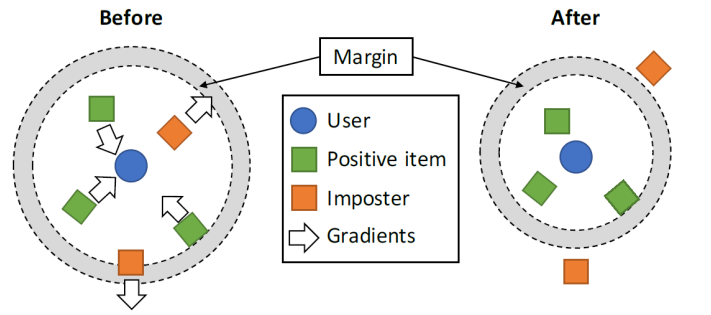
이 모델의 Loss function은 각 유저별 positive item과 negative item간의 거리가 충분해야한다는 로직 하에 구성되었다.

Knowledge Distillation
ML, DL과 같은 복잡한 모델들이 점점 인기를 끌었지만, 복잡한 모델들은 필요로 하는 파라미터도 많아져 모델 효율성 이슈가 발생했다.
위 같은 큰 규모의 모델들은 많은 파라미터를 요구하기도 하여, 연산시간이나 메모리 비용이 꽤 크다.
이에 따라 점차 단기간 추론 시간을 들이고도 높은 성능을 낼 수 있는 모델에 대한 니즈가 증가했다.
즉 취지는 정확도가 높으면서도 사이즈는 작은 모델을 만들고자 하는 것이다. Knowledge distillation은 두 가지 모델을 만들게 된다. 선생님(teacher) 별칭을 가진 큰 모델 하나와, 학생(student) 별칭을 가진 작은 모델이다. student모델은 teacher모델에서 알려준 정보로 추론하게 된다. 즉 학습은 teacher 모델로 진행하고, 추론은 student 모델로 진행하는 것이다.
예를 들어 판다 사진을 주고, teacher모델이 학습하게 되면 "panda"라고 분류하지만, 그 외 다른 class에 대해 예측 점수도 반환하게 된다. 이 정보를 teacher의 지식(knowledge)라고 하고, 이 지식을 student 모델로도 공유하게 된다. 즉 teacher는 pre-train하는 모델이고, soft lable 즉 모든 class에 대한 추론 점수를 반환하여 student모델에 주게 되면, student모델은 "panda", "no panda"라는 binary, 즉 hard label 과 teacher에게 받은 soft label 두 정보를 사용하여 학습하게 된다.
Ranking Distillation이라는 알고리즘을 살펴보자.
teacher 모델과 student 모델을 모두 생성하게 된다. teacher모델은 학습된 결과를 K개의 class 마다 예측확률을 추론하게 된다.
이 추론 결과에서 Top K번째까지의 아이템을 골라 hard label을 하게 된다. (예측 점수가 높은 K개 아이템에 대해서만 정답지로 여김)
이 Hard label을 바탕으로 student 모델은 학습하게 된다. 안타깝게도 이 방식은 추론 시간을 생각보다 줄일 수 없다고 한다.
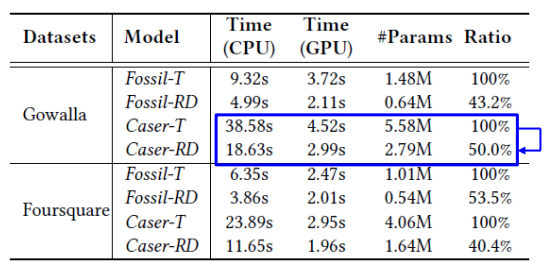
논문에서 소개하는 Ranking Distillation vs Teacher 모델 추론 속도
Ranking Distillation의 단점을 몇 가지 보완한 다른 알고리즘들도 있다. 그 중 하나가 Collaborative Distillation인데,
RD가 soft label에서 참고할만한 몇몇 중요한 정보들을 생략한다는 이슈가 있어 삭제된 데이터를 확률론적으로 재사용하자는 것이다.
높게 ranked된 아이템과 낮게 ranked된 아이템 중 샘플링하여 사용하고, high rank는 그대로 1로 매기되, low rank는 그 값을 그대로 사용하자는 것이다.
또 다른 논문(Bidirectional Distillation, BD)에서는 다른 접근 방식을 지니는데, student 모델이 꼭 teacher모델보다 우위에 있다고 할 수 없다는 것이다. 또한 high-ranked된 아이템에서 얻을 수 있는 정보가 꼭 기대한 만큼 정보성(informative)이 높지 않다는 것이다.
따라서 teacher모델도 student모델의 knowledge를 학습하는 방식으로 서로 모델을 참조(동시학습)하도록 구조를 변경하자는 주장을 한다.
대신 student 모델에서 예측력이 어느 정도 이상인 knowledge만을 teacher로 넘기게 된다.