| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- transformer
- 자연어처리
- AWS
- 클라우드
- BERT
- 추천시스템
- 머신러닝
- 네트워크
- docker
- 합격후기
- nlp
- 미국 개발자 취업
- MLOps
- 언어모델
- BANDiT
- llm
- chatGPT
- BERT이해
- 미국석사
- 플랫폼
- MAB
- RecSys
- maang
- HTTP
- 클라우드자격증
- TFX
- MSCS
- 중국플랫폼
- swe취업
- 메타버스
- Today
- Total
SWE Julie's life
Contextual Bandit - 플랫폼 추천시스템 알고리즘, MO-LinCB 본문
Introduction
여러 이해 관계자들이 존재하는 플랫폼의 추천 시스템은 하나 이상의 최적화 문제를 풀어야한다.
흔히 최적화를 할 때 극대화 혹은 최소화하고자 하는 '목적 함수(objective)'가 있는데, 이 목적 함수가 여럿이라는 것이다.
여기서 목적함수의 개념은 유저의 행동 metric (ex) 클릭, 스트리밍, 체류시간 등), 혹은 플랫폼의 프로모션과 같은 자체 목적 등이 포함된다.
이러한 여러 가지의 metric을 동시에 만족시키기란 현실적으로 힘들다.
따라서 본 논문은 다중 이해관계자가 존재하는 플랫폼 상에서의 다중 목적 최적화 문제를 contextual bandit으로 해결하고자 한다.

일반적으로 다중 목적 최적화 (multi-objective optimization) 을 해결하는 데에 있어 GGI (Generalized Gini Index)함수를 사용한다.
GGI란 지니계수를 일반화(generalize)한 지표인데, MAB 알고리즘 중 다중 목적 함수 최적화를 위해 주로 사용되는 함수이다.
여러 목적 함수들을 결합하고 조정하여 GGI 지표로 집계하는 것이다.
GGI에 대한 자세한 설명은 아래 논문을 참고하면 좋을 것이다 :
Multi-objective Bandits: Optimizing the Generalized Gini Index
http://proceedings.mlr.press/v70/busa-fekete17a/busa-fekete17a.pdf
본 논문 역시 GGI 함수를 이용하여 스케일(scalarised)된 여러 목적 함수들에 대한 보상들을 gradient ascent 알고리즘으로 극대화한다.
Amazon, Facebook, Uber와 같이 플랫폼은 아래와 같이 세 가지 조건을 동시에 충족하는 운영 정책을 보유해야한다.
1. 플랫폼 공급자로서 플랫폼 수익을 최적화
2. 소비자의 만족도를 최적화
3. 공급자의 만족도를 최적화
순차적(Sequential)으로 의사결정이 이루어지는 점과, 여러 변수(variant)를 보유하고 있다는 점에서 MAB문제와 유사하다고 볼 수 있다.
따라서 많은 논문들이 MAB알고리즘을 통해 탐색(exploration)과 수확(exploitation)의 양자택일 문제에서 플랫폼 의사결정을 지원하고자했다.
전통적인 bandit 환경은 시스템이 매 action을 수행한 이후 단일 수치형(scalar) 보상만을 지급받는다고 가정하고 있지만,
다중 목적 환경에서의 시스템은 반드시 여러 기준들의 최적화 (joint optimization)을 동시에 이루어내야한다.
따라서 본 논문은 contextual bandit 알고리즘을 통해 다중 이해관계자가 존재하는 플랫폼 맞춤형 다중 목적성 contextual bandit 알고리즘을 소개한다.

논문은 본격적으로 알고리즘을 다루기전에, 목적 함수에 대한 선행 분석 결과를 소개한다.
유저 중심적인 metric (클릭, 플레이 횟수 등)과 공급자 중심적인 metric (소비자 풀 다양성), 플랫폼의 promotion과 같은 목적 함수들 간의 상관관계를 분석하고, 몇 가지 insight를 도출해냈다.
그 결과 두 가지 사실을 알아낼 수 있었는데, 하나는 여러 목적 함수들은 서로 어느 정도 수준의 상관관계를 지니고 있다는 것이다.
다른 하나는 하나의 목적 함수를 최적화 하는 것이 다른 목적 함수에 오히려 마이너스의 효과를 줄 수 있다는 것이다. (음의 상관관계)
Key Notions
알고리즘에 사용되는 주요 개념들의 notation을 정리하자면 아래와 같다.
- context : 𝓣
- action : a (총 K개 존재)
- reward : 𝒙 ([0,1] 구간 내 존재, D(𝒙 | 𝓣) 분포의 sample )
각 bandit은 round t에 feature set 𝓣[t]를 받게 된다. 각 원소는 M 차원이다.
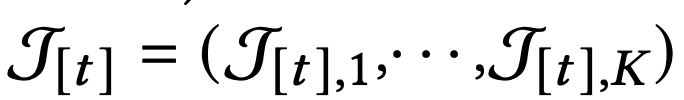
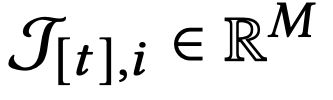

보상함수는 transposed된 context 벡터와 MxD차원 파라미터의 곱값에 D차원 random noise의 합으로 구성되어있다.
동일 전략(strategy)에 대해 어느 정도 데이터가 수집되면, 평균 보상값을 계산할 수 있는데, 이 계산식은 아래와 같다.
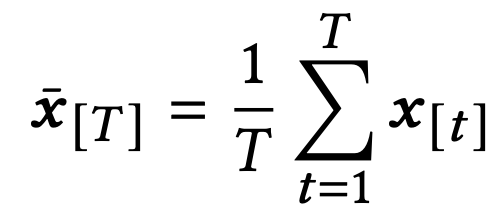
앞서 언급되었듯이, 다중 목적 최적화 문제에서 다중 목적 함수들을 GGI (Generalized Gini Index) 집계함수를 사용하여 표현한다고 하였다.
이러한 G(x[t])를 극대화하는 전략을 찾는 것이 본 알고리즘의 목표이다.
정리하자면 아래와 같이 총 K개 arm에 대해 가장 max 값을 가져다줄 수 있는 𝛂*를 찾는 것이 알고리즘의 전체이다.
여기서 𝛂*는 single arm이 아니라 K개 arm 각각에 대한 확률 분포를 제안하는 전략을 의미한다. (𝛂k가 단일 arm에 해당)
따라서 이를 논문에서는 혼합전략(mixed strategy)라고 부른다.
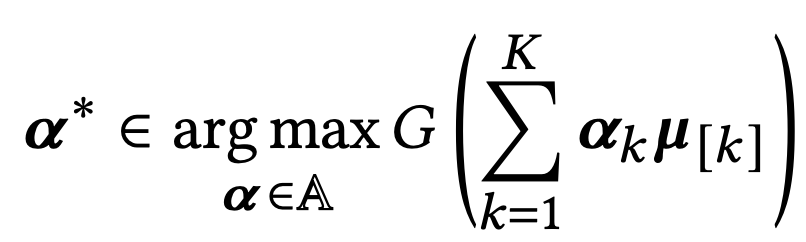

GGI 연산은 아래와 같은 식으로 이루어진다. (보상 벡터 𝒙 = ( 𝒙1, ... , 𝒙D))
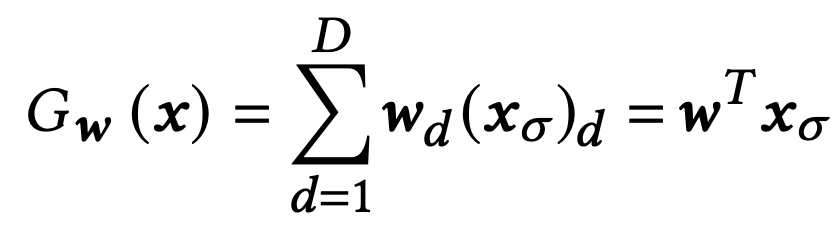
앞서 우리가 𝒙에 대해 정의할 때 unknown parameter로 지정한 𝛝라는 값을 알고 있다고 가정했을 때,
optimal mixed policy 𝛂*는 아래와 같이 다시 재정의될 수 있다.
이 때 noise term은 round T가 충분히 클 때, 평균적으로 0에 가깝다고 가정하고 생략되었다.
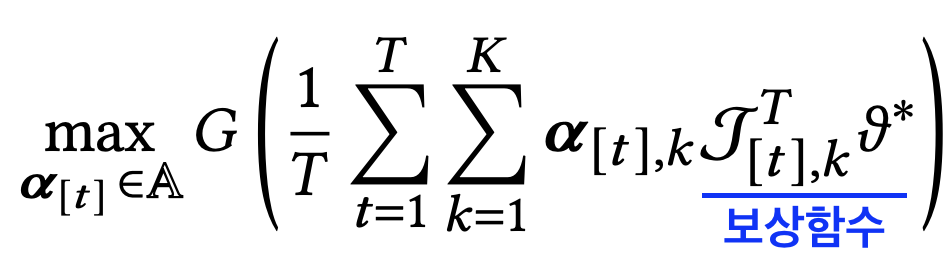
위 식에 따라 Regret (예측값과 실제 optimal값의 차이) 에 대한 식도 아래와 같이 정의가 가능하다.

여기서 𝛂[t]는 round t에 추천된 action이다.
눈여겨봐야할 점은, 모델 성능이 평균 보상의 집계 함수 값으로 결정된다는 것이다. (보상의 집계함수 합의 평균이 아님)
Learning Algorithm
알고리즘은 regret을 줄이는 방향으로 학습해나가야한다. 논문의 학습 알고리즘은 MO-LinCB라고 지칭한다.
앞서 𝛝*에 대해 알고 있다는 가정 하에 식을 풀어나갔었는데, 𝛝*에 대한 추정값을 아래 식에 대해 ridge regression을 통해 구한다.
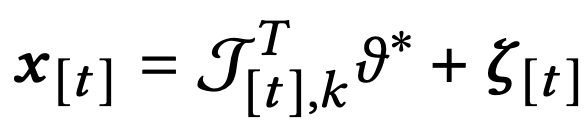
또한 집계함수값을 최대화하는 과정에 있어 gradient ascent 알고리즘을 사용한다.
아래 값을 최대화하는 𝛂[t]를 찾아내야하는데, 이 때 GGI 의 오목성을 이용한다.

G(x) 함수의 오목성(concavity)에 따라 아래와 같이 정의가 가능하여, 좌항을 gradient ascent를 통해 최적화하는 문제로 대신할 수 있다.

위 과정을 pseudo-code로 풀면 아래와 같다.

Conclusion
플랫폼은 여러 유형의 이해관계자들이 존재하는 공간이다.
각각이 추구하는 목적과 가치가 다르기 때문에, 플랫폼에서 모두를 만족시킬만한 추천 시스템을 운영하기 위해서는 다중 목적 최적화가 필요하다.
하지만 하나의 목적이 다른 목적과 매우 유사하거나 혹은 충돌할 수도 있다.
이러한 상황을 고려하여 논문은 MO-LinCB라는 알고리즘을 소개한다.
Contextual Bandit 알고리즘 계열이며, 다중 목적 함수들의 Gini 계수 값을 최대화하는 데에 있어 gradient ascent 알고리즘을 사용한다.
GGI 기반 로직은 총 보상을 극대화할 뿐만 아니라, 다른 목적 함수들간의 balance를 맞추는 데도 적절하다.
굉장히 신선한 접근이었다. 요즈음 대부분의 서비스들은 플랫폼이 되고자 하며, 그를 통해 누릴 수 있는 독점성을 무척 원한다.
이러한 사회적 상황에서 플랫폼의 본질인 양면시장을 정확히 관철하였고, 여러 플레이어들의 만족도를 고루 충족할 수 있는 알고리즘을 소개했다.
하지만 Contextual Bandit 계열이라고 소개되었음에도 구체적으로 어떤 Context를 어떻게 반영하였는지는 소개되어있지 않은 듯 하다.
알고리즘 상에서도 Context feature가 있지만, 구체적으로 어떻게 가공되어 사용되는 것인지 파악하기가 어려웠던 점이 조금 아쉬웠다.
