불균형(imbalanced) 데이터 모델링은 ROC curve를 사용을 추천하지 않는 이유

이번 글은 모델링 영역 중에서도 모델 성능 고도화를 위한 일종의 팁 같은 글이 될 것 같다.

​

우리는 데이터 과제를 하다 보면 불균형 데이터셋을 접할 일이 굉장히 많다. 여기서 말하는 불균형이란, 클래스 비중이 다르다는 것이다. 예를 들어 이진 분류 문제일 경우 0인 클래스와 1인 클래스를 분류하게 되는데, 일반적으로 우리가 추론하고자 하는 타겟 클래스인 1 클래스는 0 클래스에 비해 데이터 수가 적다. 단순히 생각하면 모델은 학습 데이터량이 많을 수록 좋은데, 데이터가 적은 경우 우리가 원하고자 하는 정답을 모델이 찾기 어려워지는 것이다. 모델이 Anomaly Detection과 같이 이상치를 분류하는 거라면 상황은 더 심각해진다.

​

모델을 설계하다보면 늘 '샘플링'의 고민을 마주하게 된다. 학습데이터의 경우 추론할 실제 데이터셋의 분포와 다른 분포를 갖고 있다면 모델을 아무리 열심히 잘 만들더라도 모델의 실제 성능은 좋지 못하다. 하물며 모델의 성능을 확인하기 위한 대조군을 설정할 때에도 실험군과 분포가 다를 경우 대조군을 적절히 선별하지 못하여 발생하는 문제를 겪게 된다. 마찬가지로 클래스의 데이터 비중도 차이가 발생할 경우 모델이 충분히 학습할 수 있도록 다른 조치를 취해주어야한다.

​

이 때 흔히 3가지의 테크닉을 이용하게 된다:

1) 소수 클래스의 데이터 량을 임의로 늘린다.

2) 다수 클래스의 데이터 량을 임의로 줄인다.

3) 모델이 소수 클래스를 올바르지 못하게 학습할 경우 penalty를 준다, 즉 클래스별 가중치를 준다.

​

이번 글은 1,2,3보다는 모델 학습시 어떤 metric을 선정할 것인지에 대해 이야기할 것이다. 결론부터 말하자면 불균형 데이터셋에서의 모델의 성능은 Precision, Recall을 트래킹하는 것을 추천하고, 이를 조화평균한 F1 Score를 Metric으로 삼아 ROC Curve보다는 PR Curve로 성능을 평가하는 것이 좋다.

​

글을 본격적으로 시작하기에 앞서 이 글은 데이터가 두 클래스를 얼마나 잘 구분하느냐보다는, 소수 클래스를 얼마나 탐지해낼 수 있느냐에 좀 더 초점이 맞춰져있다는 걸 염두할 필요가 있다. 우리는 데이터를 두 그룹으로 나누는 데에도 분류를 사용할 수 있지만, 정상 집단에서 비정상 집단을 탐지하는 것 처럼 특정 집단을 찾는 데에 더 중점을 두어 분류를 사용할 수 있다. 만약 모델이 1인 클래스를 좀 더 정확히, 더 많이 탐지해내길 바란다면 이번 글이 도움이 될 수 있다.

​

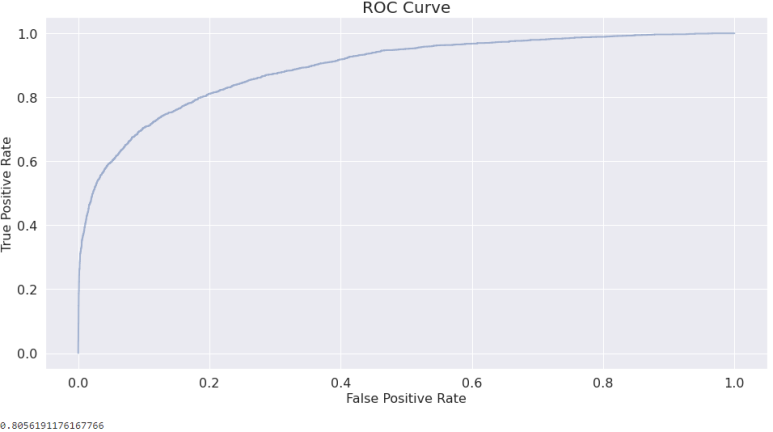
우리는 모델 성능을 보여주는 값으로 AUC를 많이 사용한다. AUC는 ROC Curve의 면적값이다. 근데 imbalanced dataset (불균형 데이터셋) 에서는 ROC보다는 PR Curve를 권장한다. 왜일까?

​

ROC Curve는 두 축으로 구성되어있다 :

TPR (True Positive Rate) = # True positives / # positives = TP / (TP+FN)

FPR (False Positive Rate) = # False Positives / # negatives = FP / (FP+TN)

여기서 TPR은 Recall과 동일한 지표이다.

ROC Curve

 

PR Curve를 생각해보자. PR Curve는 Precision과 Recall인데, 각각에 대한 정의는 아래와 같다.

Precision, Recall은 기본적인 개념이라 간단히만 설명하고 넘어가자면 Precision은 내 모델이 예측한 클래스가 실제 클래스와 얼마나 일치하는가에 관한 이야기이고, Recall은 내 모델이 실제 클래스 중 얼마나 정확히 클래스를 분류하였는가에 관한 이야기이다. 그리고 이 둘은 서로 상충하는 관계이다. Precision을 높이다보면 Recall이 떨어지고, Recall을 높이다보면 Precision을 잃을 수 밖에 없다. 극단적으로 생각해보면 모든 클래스를 전부 1로 예측하면 Recall은 높지만 (실제 1인 클래스를 얼마나 1로 분류하였는지) Precision은 (1로 예측한 클래스 중 실제 1이었던 경우의 수)은 처참할 수밖에 없다. Precision은 좀 더 보수적으로 접근하게 된다.

Precision =# True positives / # predicted positive = TP/(TP+FP)

Recall = # True positives / # positives = TP / (TP+FN)

​

ROC Curve에서 TPR이 Recall과 동일하다는 것을 생각하면 ROC Curve와 PR Curve의 차이는 FPR과 Precision의 차이만 존재한다. 그럼 FPR과 Precision을 좀 더 보자.

Precision =# True positives / # predicted positive = TP/(TP+FP)

FPR = # False Positives / # negatives = FP / (FP+TN)

​

식에서도 볼 수 있듯 FPR은 Total Negatives 가 분모로 존재하기 때문에 총 Negative Class의 수가 FPR값에 큰 영향을 미친다. 즉 Imblanaced Dataset에서는 Negative 클래스인 0 클래스 수가 1클래스 수에 비해 워낙 많은 상황이기 때문에 False Positive의 수가 개선되더라도 FPR 값이 줄기 쉽지 않다. 반면 Precision은 전체 negative class 수에 전혀 영향을 받지 않게 된다. 따라서 FPR을 활용하는 AUC스코어보다는 F1 Score를 활용하여 학습한 뒤 PR Curve를 통해 모델의 성능을 검증하는 것이 좋다.

​

정리하자면 Precision은 클래스 1에 대해 정확하게 탐지할 수 있는 확률을 계산하지만, FPR과 TPR은 클래스를 분간하는 능력을 지표화하는데 초점이 맞춰져있다.

​

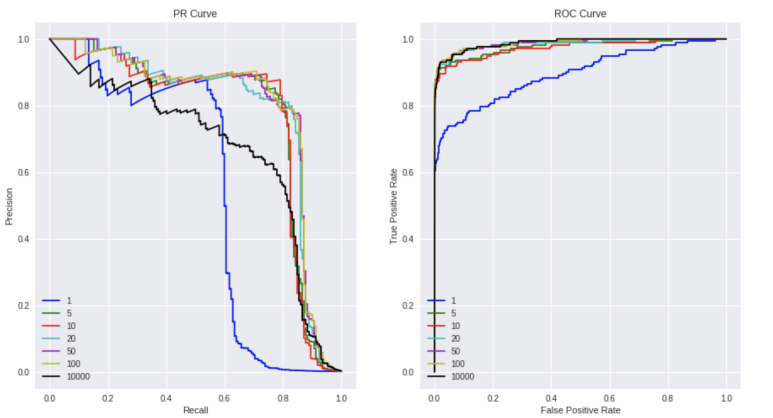
실제로 동일한 데이터에 대해 AUC로 metric을 삼느냐 F1으로 삼느냐에 따라 1에 대한 Recall, Precision값 개선 정도가 다르다. 이를 시뮬레이션한 자료는 아래 참고자료에 두 링크를 참조하는 것이 좋다. 아래 그림을 보면 동일한 색이 동일한 파라미터로 학습한 모델의 결과인데, PR Curve와 ROC Curve에서의 순위가 각각 다른 경우가 있다는 것을 알 수 있다.

출처 :  https://www.kaggle.com/code/lct14558/imbalanced-data-why-you-should-not-use-roc-curve/notebook

 

---

 

참고자료

https://www.kaggle.com/code/lct14558/imbalanced-data-why-you-should-not-use-roc-curve/notebook

 

https://towardsdatascience.com/what-metrics-should-we-use-on-imbalanced-data-set-precision-recall-roc-e2e79252aeba